10. Parameters
Parameter Sharing
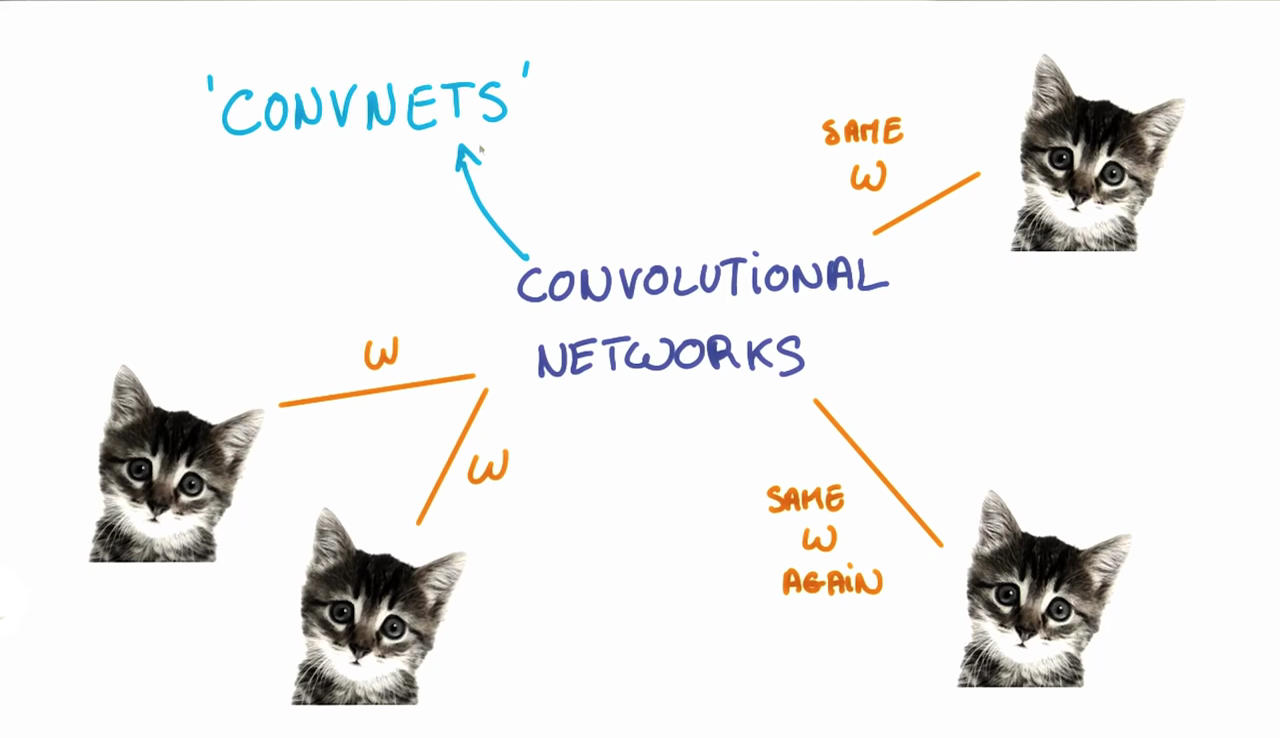
The weights,
w
, are shared across patches for a given layer in a CNN to detect the cat above regardless of where in the image it is located.
When we are trying to classify a picture of a cat, we don’t care where in the image a cat is. If it’s in the top left or the bottom right, it’s still a cat in our eyes. We would like our CNNs to also possess this ability known as translation invariance. How can we achieve this?
As we saw earlier, the classification of a given patch in an image is determined by the weights and biases corresponding to that patch.
If we want a cat that’s in the top left patch to be classified in the same way as a cat in the bottom right patch, we need the weights and biases corresponding to those patches to be the same, so that they are classified the same way.
This is exactly what we do in CNNs. The weights and biases we learn for a given output layer are shared across all patches in a given input layer. Note that as we increase the depth of our filter, the number of weights and biases we have to learn still increases, as the weights aren't shared across the output channels.
There’s an additional benefit to sharing our parameters. If we did not reuse the same weights across all patches, we would have to learn new parameters for every single patch and hidden layer neuron pair. This does not scale well, especially for higher fidelity images. Thus, sharing parameters not only helps us with translation invariance, but also gives us a smaller, more scalable model.
Padding
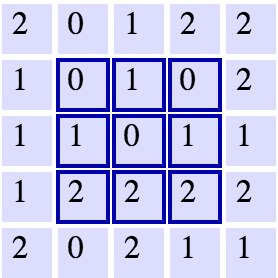
A
5x5
grid with a
3x3
filter. Source: Andrej Karpathy.
SOLUTION:
3x3As we can see, the width and height of each subsequent layer decreases in the above scheme.
In an ideal world, we'd be able to maintain the same width and height across layers so that we can continue to add layers without worrying about the dimensionality shrinking and so that we have consistency. How might we achieve this? One way is to simply add a border of
0
s to our original
5x5
image. You can see what this looks like in the below image.
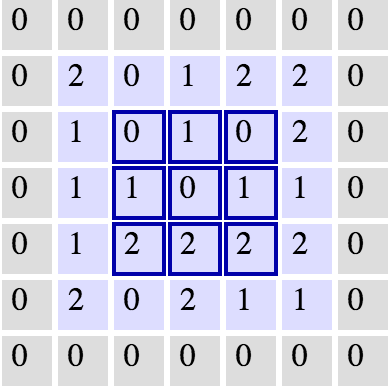
The same grid with
0
padding. Source: Andrej Karpathy.
This would expand our original image to a
7x7
. With this, we now see how our next layer's size is again a
5x5
, keeping our dimensionality consistent.
Dimensionality
From what we've learned so far, how can we calculate the number of neurons of each layer in our CNN?
Given:
-
our input layer has a width of
Wand a height ofH -
our convolutional layer has a filter size
F -
we have a stride of
S -
a padding of
P -
and the number of filters
K,
the following formula gives us the width of the next layer:
W_out =[ (W−F+2P)/S] + 1
.
The output height would be
H_out = [(H-F+2P)/S] + 1
.
And the output depth would be equal to the number of filters
D_out = K
.
The output volume would be
W_out * H_out * D_out
.
Knowing the dimensionality of each additional layer helps us understand how large our model is and how our decisions around filter size and stride affect the size of our network.